भूमिका
गणित ‘अमूर्त विज्ञान’ है। यह विज्ञान और तकनीकी का मेरूदण्ड है। लगथ मुनि कृति ‘वेदांग ज्योतिष’ में गणित के महत्व को इस तरह रेखांकित किया गया है :
“यथा शिखा मयुराणाम् नागानाम् मणयो यथा।
तद्वत् वेदांग शास्त्राणाम् गणितम् मूर्धनिस्थितम्॥”
( अर्थात् सभी वेदांग शास्त्रों के शीर्ष पर गणित उसी प्रकार सुशोभित है जैसे मयूर के शिर पर शिखा और नाग के फन पर मणि सुशोभित है। )
हड़प्पा सभ्यता और गणित
हड़प्पा लिपि के वाचन न हो पाने के कारण उनके सैद्धांतिक पक्ष की जानकारी का बस अनुमान ही लगाया जा सकता है। परन्तु वहाँ से जो भौतिक अवशेष मिले हैं उनसे गणित के विकास का अनुमान लगाया जा सकता है।
- पूरे हड़प्पा सभ्यता में माप-तौल का मानकीकरण अद्वितीय है।
- बाँटों की प्रमुख विशेषता उनका ‘घनाकार’ और ‘सोलह के गुणजों’ में प्रयोग था। बाँट एक शृंखला में क्रमशः बढ़ते जाते थे, पहले वे १, २, ४, ८, १६ से ६४ तक ‘दोगुने’ होते जाते थे और उसके बाद १६० से आगे ‘१६ के दशमिक गुणजों’ में बढ़ते थे; यथा – ३२०, ६४०, १६००, ६४०० ( १६०० × ४ ), ८००० ( १६०० × ५ ), १२८००० ( १६००० × ८ ) आदि।
- इनको द्विभाजन / द्विचर प्रणाली ( binary system ) और दशमलव प्रणाली ( decimal system ) की जानकारी थी। मापन के निचले स्तर पर बाँटों में द्विभाजन पद्धति का और ऊपर के स्तर पर दाशमिक पद्धति के प्रयोग का प्रमाण मिलता है। ये बाँट घनाकार होते थे जोकि मुख्यतः चकमक प्रस्तर ( flint or fire stone ) से निर्मित होते थे।
- लम्बाई की माप फुट ( ३७·६ सेंटीमीटर ) और क्युबिट / हाथ ( ५१·८ से ५३·६ सेंटीमीटर ) पर आधृत थी।
- ध्यान देने वाली बात है कि आधुनिक काल तक भारतीय समाज १६ और १६ के गुणजों का प्रयोग मापन में करता रहा है। १ रुपया में १६ आना होता है। सोलह छटाँक का एक सेर होता है। कहावतों में शत-प्रतिशत शुद्धता के लिए ‘सोलह आना खरा’ शब्द का प्रयोग किया जाता है। भूमि उर्वरता चार आना, आठ आना और सोलह आना जैसे मानकों में मापी जाती है।
- लम्बाई के मापन के लिए पटरी ( scale ) का प्रयोग किया जाता था।
- जिल तरह से नगर बसाया गया था और ईंटों का मानकीकरण ( १ : २ : ४ ), मुहरों का मानकीकरण ( २·८ × २·८ सेंटीमीटर ) आदि से विकसित रेखागणित का ज्ञान होता है।
वैदिक और सूत्रकालीन गणित
वैदिक काल से ही हम गणित के विकसित होने का प्रमाण पाते हैं। गणित के विकास के लिए सूत्र-काल ( ६०० ई॰ पू॰ – ३०० ई॰ पू॰ ) महत्त्वपूर्ण है।
गणित शब्द ‘गण्’ धातु में ‘क्त्’ प्रत्यय लगाने से बना है।
गणित शब्द वैदिक साहित्य में अपने मूल रूप में अप्राप्य है। हालाँकि गण, गणपति जैसे शब्द ऋग्वेद में मिलते हैं। गणित शब्द का प्रथम प्रयोग लगथ मुनि कृति वेदांग ज्योतिष में मिलता है : ( यथा शिखा मयुराणाम् नागानाम् मणयो यथा। तद्वत् वेदांग शास्त्राणाम् गणितम् मूर्धनिस्थितम्॥)
वैदिक आर्यों ने गणित का विकास नक्षत्रविद्या के अनुषंगी विषय के रूप में किया। इस काल में यज्ञ करने के लिए शुभ समय के लिए ग्रह-नक्षत्रों की गणना के लिए गणित का प्रयोग किया जाता था। यज्ञ वेदी के निर्माण के लिए नाप-जोख की जाती थी। इस तरह ज्योतिष विद्या के अनुसार गणित का विकास हुआ।
सूत्र साहित्य के ‘कल्पसूत्र’ के अन्तर्गत आने वाला ‘शुल्व-सूत्र’ विशेष महत्त्व का है। शुल्व का अर्थ है — नापना। यज्ञों में विभिन्न आकृति की वेदियाँ और मण्डप बनाये जाते थे। इन्हीं वेदियों व मण्डपों की नाप-जोख के लिए शुल्व सूत्रों का विकास हुआ। ये सूत्र भारतीय गणितशास्त्र के ‘प्राचीनतम् ग्रंथ’ कहे जा सकते हैं। इनमें हम ज्यामिति ( रेखागणित ) को अत्यन्त विकसित अवस्था में पाते हैं।
ज्यामितीय विकास की दृष्टि से बौधायन ( ८०० ई॰पू॰ ) विशेष रूप से उल्लेखनीय हैं। प्रसिद्ध शुल्व सूत्र ( बौधायन प्रमेय ) इन्होंने ही दिया। इसके अतिरिक्त √२ जैसी संख्याओं का मान, वृत्त से वर्ग और वर्ग से वृत्त में बदलने का नियम इन्होंने दिया। ये विविध ज्यामितीय आकृतियों – त्रिभुज, आयत, समलम्ब चतुर्भुज आदि से परिचित थे।
यजुर्वेद में ऋषि मेधातिथि कृत अग्नि की स्तुति में ये श्लोक आता है :—
“इमा मे अग्नइष्टका धेनवः सन्त्वेका च दश च दश शत्रं च शतं च सहस्त्रं च सहस्त्रं चायुतं चायुतं च नियुतं च प्रयुतं च चार्बुदं च न्यर्बुदं च समुद्रश्च मध्यं चान्तश्य परार्धश्चैता।”
- ( इस श्लोक से स्पष्ट है कि — एक ( १ ), दस ( १० ), शत ( १०० = १०२ ), सहस्त्र ( १,००० = १०३ ), अयुत ( १०,००० = १०४ ), नियुत ( १,००,००० = १०५ ), प्रयुत ( १०,००,००० = १०६ ), अर्बुद ( १,००,००,००० = १०७ ), न्यर्बुद ( १०,००,००,००० = १०८ ), समुद्र ( १,००,००,००,००० = १०९ ), मध्य ( १०,००,००,००,००० = १०१० ), अन्त ( १,००,००,००,००,००० = १०११ ) और परार्ध ( १०,००,००,००,००,००० = १०१२ ) जैसी संख्याओं का उल्लेख है। )
‘विष्णु पुराण’ में उल्लेख मिलता है कि एक स्थान से दूसरे स्थान का मान दस गुणा होता है अठारहवें स्थान को ‘परार्ध’ कहते हैं।यहाँ ध्यान देने वाली बात यह है कि १०१७ लिए परार्ध शब्द ब प्रयुक्त हुआ है।
प्रथम शताब्दी ई॰पू॰ के जैन ग्रंथ ‘अनुयोगद्वार सूत्र’ में गणना के लिए असंख्येय संख्या का उल्लेख हुआ है जिसका मान १०१४० के बराबर है।
ध्यातव्य है कि :—
- चौथी शताब्दी तक यूनानियों को १०४ ( Myraid ) और रोमवासियों को पाँचवीं शताब्दी तक १०३ ( Milley )तक की संख्या का ही ज्ञान था।
- वहीं भारतीयों को १०५३ ( तल्लक्षणा ), १०६० ( महौघ ) और १०१४० ( असंख्येय ) जैसी बड़ी संख्याओं का ज्ञान था।
साहित्यों में संख्याओं के विभाजन और उनके सूक्ष्म प्रयोग इस तरह मिलते हैं :—
- १ ÷२ ( अर्ध ),
- १ ÷ ४ ( पाद ),
- १ ÷ ८ ( शफ ),
- १ ÷ १२ ( काष्ठा ),
- १ ÷ १६ ( कला ) आदि।
“अतः दाशमिक पद्धति का ज्ञान वैदिक भारतीयों को था।”
परन्तु अंक चिह्नों के साथ इस पद्धति के प्रयोग का साक्ष्य बक्षाली पाण्डुलिपि ( तृतीय – चतुर्थ शताब्दी ईसवी ) से मिलता है। बक्षाली पेशावर के समीप एक स्थान है। इस पाण्डुलिपि की प्राप्ति १८८१ ई० में हुई थी। समकालीन गणित पर प्रकाश डालने वाला यह एकमात्र ग्रंथ है।
वैदिक गणित पर अभिनव कार्य
स्वामी भारती तीर्थकृष्ण ने ‘वैदिक गणित’ नामक पुस्तक लिखी। इसमें उन्होंने १६ सूत्रों और १३ उपसूत्रों का का विवरण उनके गुणधर्म और प्रयोगों के साथ दिया है।
वर्ग ज्ञात करने की विधि :
( १ ) सूत्र एकन्यूनेन पूर्वेण – ९ से बनी संख्याओं; यथा – ९, ९९, ९९९ … आदि का वर्ग इस सूत्र से सरलता से निकाला जा सकता है।
( २ ) सूत्र एकाधिकेन पूर्वेण – जिन संख्याओं में ईकाई ५ हो उनका वर्ग इस विधि से सरलतापूर्वक निकाला जा सकता है।
विविध
प्राचीन ग्रंथों में १ से लेकर १० की घात ५३ तक की संख्याओं को पृथक-पृथक नाम दिये गये हैं –
- नियुतम १०११
- उत्संग १०२१
- हेतुहीलम १०३१
- नित्रवाद्यम १०४१
- तल्लक्षणा १०५३ आदि।
समय के मापन के लिए निम्न इकाइयों का उल्लेख मिलता है-
- कृति = १ / ३४००० सेकंड
- त्रुटि = १/ ३०० सेकंड
- विपल = ०·४ सेकंड
- घड़ी = २४ मिनट
- होरा = १ घंटा
- दिवस = १ दिन
- वर्ष = १ साल
- युग = ४,३२,००० वर्ष आदि।
मेरुप्रस्तर : हलायुध ( १०वीं शताब्दी ) ने १, २, ३, ४, … आदि संख्याओं के विभिन्न समुच्चय ( combination ) प्राप्त करने की विधि दी। मेरुप्रस्तर विधि और पास्कल त्रिकोण ( १६वीं शताब्दी ) में समानताएँ हैं –
भारतीयों का गणित क्षेत्र में योगदान
भारतीय अंक संकेत
भारतीय गणितज्ञों ने गणित में अंक संकेतन की जो पद्धति निकाली उसकी कुछ विशेषताएँ थी; यथा – प्रत्येक अंक संकेत का निरपेक्ष मान, स्थानीय मान और शून्य का प्रयोग।
रोमन अंक लिपि में शून्य और स्थानीय मान का अभाव था। अतः वे बड़ी संख्याओं को नहीं लिख पाते थे।
उदाहरणार्थ – १७५९ को रोमन लिपि में लिखना हो तो :-
- १७५९ = MDCCLIX ( M = १०००, D = ५००, C = १००, L = ५०, IX = ९ )
भारतीय अंक संकेत में स्थानीय मान और शून्य के प्रयोग से बड़ी बड़ी संख्या व्यक्त करने में सुगमता होती है। इसी पद्धति को सम्पूर्ण विश्व ने अपना लिया।
बगदाद के विद्वान अलख्वारिज्मी कृत ‘हिसार अल जबर वल मुकाबलाह’ से भारतीय अंक संकेत प्रतीकों की जानकारी शेष विश्व को हुई।
भारत से यह अंक संकेत के प्रतीक अरब के माध्यम से यूरोप और शेष विश्व तक पहुँची। इसीलिए वे इसे ‘अरबी अंक प्रणाली’ मान बैठे।
अरबी विद्वान स्वयं इन अंक संकेतों को ‘हिंदसा’ या ‘अल अरकम अल हिन्द’ ( हिंद के अंक ) कहते हैं।
अब इसको हिन्दू-अरैबिक अंक प्रणाली ( Indo-Arabic Number system ) कहा जाता है। परन्तु इसका सही नाम हिन्दू अंक प्रणाली या भारतीय अंक संकेतन प्रणाली होना चाहिए।
ये अंक संकेत प्रतीकों की संख्या ‘दस’ हैं। इनका विकास ब्राह्मी लिपि से हुआ है। जो इस प्रकार हैं –
- १, २, ३, ४, ५, ६, ७, ८, ९ और ०।
- आधुनिक भारतीय संविधान के अनुच्छेद – ३४३ में संघ की राजभाषा का उल्लेख हुआ है जिसमें कहा गया है कि, ‘संघ के शासकीय प्रयोजनों के लिए प्रयोग होने वाले अंकों का रूप भारतीय अंकों का अंतर्राष्ट्रीय रूप होगा।’
- ये अंतरराष्ट्रीय रूप हैं – 1, 2, 3, 4, 5, 6, 7, 8, 9 और 10।
शून्य की खोज
शून्य वैश्विक गणित को भारतीयों द्वारा दिया गया अमूल्य उपहार है। इसकी खोज किसने की यह अज्ञात है। यद्यपि कुछ विद्वान इसका आविष्कारक वैदिक ऋषि गृत्समद को मानते हैं।
शून्य के लिए एक प्रतीक चिह्न निश्चित करने का प्रथम साक्ष्य ‘वक्षाली पाण्डुलिपि’ में मिलता है।
गणितज्ञ भास्कराचार्य ने शून्य के विषय में लिखा है – “खयोगे वियोगे धनर्ण तथैव च्युत शून्यतस्तद्विपर्यासमेति॥“
स्थानीय और निरपेक्ष मान
भारतीय अंक संकेतन पद्धति की यह प्रमुख विशेषता है। इन दस अंक प्रतीकों में से प्रत्येक का एक निरपेक्ष मान होता है और जब वह प्रयुक्त होता है तो उसका स्थानीय मान भी होता है। इसी विशेषता के कारण भारतीय अंक पद्धति वैज्ञानिक अंक प्रतीक प्रणाली सिद्ध हो सकी।
इन अंक संकेतों के ‘दोहरे मान’ होते हैं। इसे इस तरह समझ सकते हैं –
- प्रत्येक अंक संकेत का स्वयं का एक स्वतंत्र मान / मूल्य होता है जिसे निरपेक्ष मान कहते हैं। यह स्थिर होता है। स्थान परिवर्तन से इनमें बदलाव नहीं होता है।
- अंक प्रतीक का स्थान परिवर्तन से उसका मान बदलता है, इसलिए इसको स्थानीय मान कहते हैं। यह बायीं ओर दस के गुणजों में बढ़ता है।
- उदाहरण – १५५। इसमें १ और ५ का निरपेक्ष मूल्य एक और पाँच है। यह स्थिर है। इसपर स्थान का कोई प्रभाव नहीं है। स्थानीय मूल्य की दृष्टि से विचार करें तो – दायीं ओर से बायीं ओर जाने पर मान में अपने पूर्ववर्ती से दस के गुणनफल के बराबर वृद्धि होगी। ईकाई ५ का मान पाँच, दहाई पाँच का मान पचास ( ५ × १० ) और सैकड़ा १ का स्थानीय मान एक सौ ( १ × १०० ) होगा।
दशमलव या दाशमिक प्रणाली
आधुनिक संख्या पद्धति का आधार दस है। इसको दशमलव या दाशमिक पद्धति इसलिए कहते हैं क्योंकि इसमें दस प्रतीक अंकों का प्रयोग किया जाता है।
इन ( १, २, ३, ४, ५, ६, ७, ८, ९ और ० ) अंकों की सहायता से किसी भी छोटी या बड़ी संख्या को दर्शाया जा सकता है।
गणित में दशमलव पद्धति के खोजकर्ता आर्यभट्ट को माना जाता है।
वर्णांक प्रणाली
संख्या को जब अक्षर संकेतों में व्यक्त किया जाता है तो इसे ‘वर्णांक’ या ‘कूटांक’ पद्धति कहते हैं। प्राचीन गणितज्ञों और ज्योतिषों ने इसका प्रयोग किया है।
आर्यभट्ट ने बड़ी-बड़ी संख्याओं को लिखने के लिए वर्णमाला के अक्षरों का प्रयोग करके मौलिक वर्णांक प्रणाली का प्रतिपादन किया था। इसके लिए उन्होंने ‘व्यंजन वर्णों’ के लिए अंकीय मान और ‘स्वर वर्णों’ के लिए घातांक मान का निर्धारण किया।
| वर्ण – अंक | वर्ण – अंक | वर्ण – अंक | वर्ण – अंक | वर्ण – अंक |
| क – १ | च – ६ | ट – ११ | त – १६ | प – २१ |
| ख – २ | छ – ७ | ठ – १२ | थ – १७ | फ – २२ |
| ग – ३ | ज – ८ | ड – १३ | द – १८ | ब – २३ |
| घ – ४ | झ – ९ | ढ – १४ | ध – १९ | भ – २४ |
| ङ – ५ | ञ – १० | ण – १५ | न – २० | म – २५ |
| वर्ण – अंक | वर्ण – अंक |
| य – ३० | अ – १ |
| र – ४० | इ – १००१ |
| ल – ५० | उ – १००२ |
| व – ६० | ऋ – १००३ |
| श – ७० | ऌ – १००४ |
| श – ८० | ए – १००५ |
| स – ९० | ऐ – १००६ |
| ह – १०० | ओ – १००७ |
| — | औ – १००८ |
उदाहरणार्थ : —
- १२५ = ‘कखड़’
- ४६५९ = ‘घचड़झ’
- ४३,२०,००० = ख्युघृ [ ( ख + य ) उ + घ × ऋ ) = ( २ + ३० ) १००२ + ४ × १००३ = ३२ × १०,००० + ४०,००,००० = ४३,२०,००० ]
बीजगणित
आर्यभट्ट प्रथम ने एक द्विघात समीकरण का हल देकर बीजगणित की शुरुआत की परन्तु यह विधि उतनी उपयोगी नहीं थी। बीजगणित के प्रभाव से दो प्रकार की राशियाँ बनी — एक, व्यक्त राशियाँ ( १,२, ३ … आदि ) और द्वितीय, अव्यक्त राशियाँ ( क, ख, ग … आदि )। व्यक्त राशियों का अध्ययन अंकगणित के अंतर्गत और अव्यक्त राशियों का अध्ययन बीजगणित के किया जाने लगा।
आगे चलकर ब्रह्मगुप्त ( सातवीं शताब्दी ) ने इसे और व्यवस्थित किया।
भास्कराचार्य ( १२वीं शताब्दी ) ने अव्यक्त संख्याओं की संकल्पना दी। भास्कराचार्य बीजगणित की व्याख्या इस तरह करते हैं :—
“अंकगणित और बीजगणित में मुख्य अंतर यह है कि अंकगणित में व्यक्त या ज्ञात राशि की बात की जाती है जबकि बीजगणित में अव्यक्त अथवा अज्ञात राशि की बात की जाती है।”
अव्यक्त राशि को ‘बीज राशि’ भी कहते हैं इसलिए अव्यक्त गणित को बीजगणित कहा गया है।
रेखागणित
भारत में रेखागणित का विकास यज्ञवेदिकाओं के विभिन्न आकार-प्रकारों ( गोल, वर्ग, आयत, अर्धगोलाकार ) के निर्माण हेतु हुआ।
यज्ञ की इकाई एक पुरुष होती थी। इसका अर्थ यह था कि जो यज्ञकर्त्ता ऊपर हाथ उठाकर खड़ा होता था और उसकी लम्बाई नाप ली जाती थी। इस लम्बाई को वृत्त या वर्ग या आयत में बदलकर यज्ञवेदी का निर्माण किया जाता था। अतः इसको बदलने के लिए ज्यामिति / रेखागणित का विकास हुआ।
इस संदर्भ में आर्यों ने बताया कि वर्ग का क्षेत्रफल भुजा का वर्ग करके और आयत का क्षेत्रफल लम्बाई और चौड़ाई का गुणा करके निकाला जाता था।
बौधायन प्रमेय जिसे शुल्व सूत्र ( ८०० ई॰पू॰ ) भी कहते हैं, पाइथागोरस से शताब्दियों पूर्व बताया जा चुका था।
रेखागणित के विकास में कल्प वेदांग के अंतर्गत शुल्व सूत्रों का विशेष महत्त्व है। यज्ञ वेदियों के निर्माण में रस्सियों / रज्जुओं ( शुल्व ) का प्रयोग किया जाता था। सूत्र का अर्थ है ज्ञान को संक्षिप्त रूप में प्रस्तुत करना।
‘π’ का मान
आर्यभट्ट ने परिधि और व्यास के अनुपात अर्थात् π का लगभग परिमित मान निकाला था।
“चतुराधिकं शतमण्टगुणं द्वाष्टिस्तथा सह्स्राणाम्।
अयुतद्धय विष्कम्भस्य आसन्नो वृत्तपरिणाहः॥”
( अर्थात् सौ में चार जोड़कर उसे ८ से गुणा करें और उसमें ६२००० जोड़ें। यह योगफल २०००० व्यास के वृत्त की परिधि के बराबर होगा। )
पाई ( π ) = परिधि ÷ व्यास = ६२८३२ ⁄ २०००० = ३·१४१६
त्रिकोणमिति
त्रिकोणमिति गणित की वह शाखा है जिसमें त्रिभुज की भुजाओं और कोणों के सम्बन्ध का अध्ययन किया जाता है।
‘ज्या’ और ‘कोज्या’ और ‘उत्क्रमज्या’ का प्रतिपादन भारतीयों ने किया जिन्हें वर्तमान में क्रमशः sine, cosine और versine कहा जाता है।
आर्यभट्ट ने ‘अर्ध-ज्या’ शब्द का प्रयोग अर्ध-जीवा के लिए किया जो बाद में ज्या और जीवा बन गया। जब यह अरबी में पहुँचा तो जीवा का जीबा हो गया। वहाँ से लैटिन में sinus ( अर्थ – अर्ध वक्र ) अनुदित करके पहुँचा। सर्वप्रथम एडमंड गुंटूर ( १५८१ – १६२६ ई॰ ) ने इसे संक्षिप्त नाम ‘sin’ दिया। इस तरह ‘ज्या’ शब्द का प्रयोग सबसे पहले आर्यभट्ट ने किया जिसे अब ‘sine’ कहा जाता है।
आर्यभट्ट ने ‘कोटिज्या’ शब्द का प्रयोग किया जो बाद में ‘कोज्या’ बन गया। जोनस मूरे ( १६७४ ई॰ ) ने इसे ही संक्षिप्त नाम ‘cos’ दिया।
भास्कराचार्य ने गोलाध्याय में ज्या ( sine ), कोटिज्या ( cosine ) और स्पर्शज्या ( tangent ) शब्द का प्रयोग किया है। इस कार्य को और आगे विकसित करने का श्रेय नीलकंठ सोमसुत्वन ( १५०० ई॰ ) को है।
कुछ प्रसिद्ध भारतीय गणितज्ञ
बौधायन
बौधायन का आविर्भाव समय लगभग ८०० ई॰पू॰ माना जाता है। इन्होंने बौधायन प्रमेय दिया जिसे शुल्व सूत्र भी कहते हैं। आजकल जिसे पाइथागोरस प्रमेय कहते हैं वह वास्तव में इनकी देन है क्योंकि बौधायन, पाइथागोरस के पूर्ववर्ती थे।
“दीर्घ चतुरस्त्र अक्षण्या रज्जुः पार्श्वमानी तिर्यक् मानी च,
यत पृथग्भूते कुरूतः तत् उभयं करोति ( इति क्षेत्र ज्ञानम )॥”
( अर्थात् एक आयत के विकर्ण पर बने वर्ग का क्षेत्रफल आयत के दोनों भुजाओं पर बने वर्गों के क्षेत्रफलों के योग के बराबर होता है। )
बौधायन का योगदान :—
- √२ जैसी संख्याओं को अपरिमेय मानते हुए उनका अधिकतम् शुद्ध मान ज्ञात किया था।
- जिसे हम पाइथागोरस प्रमेय कहते हैं वह वास्तव में बौधायन ने उनसे पूर्व ही दिया था।
- बौधायन ने वृत्त को वर्ग, वर्ग को वृत्त में बदलने का नियम दिया।
- बौधायन त्रिभुज, आयत, समलम्ब चतुर्भुज जैसी ज्यामितीय आकृतियों से परिचित थे।
आर्यभट्ट
गुप्तकाल गणित के विकास की दृष्टि से उल्लेखनीय है। इस समय की विभूति गणितज्ञ आर्यभट्ट थे। इनकी कृति ‘आर्यभट्टीयम्’ है।
- इन्होंने अंकगणित, बीजगणित, ज्यामिति और त्रिकोणमिति के सिद्धान्त दिये।
- यह कृति वृत्तों, त्रिभुजों, चतुर्भुजों और ठोसों के कुछेक प्रमुख गुणों का उल्लेख करती है।
- ‘वृत्तफलं समपरिणाहस्यार्ध विष्कम्भार्धहतमेव।’ अर्थात् वृत्त का क्षेत्रफल परिधि और व्यास के आधे के गुणनफल के बराबर होता है ( १ ⁄ २ परिधि × १ ⁄ २ व्यास )।
- ‘त्रिभुजस्य फलं शरीर समदलकोटि भुजार्थ सवर्गः।’ अर्थात् त्रिभुज का क्षेत्रफल उसके आधार और समान कोटी के गुणनफल का आधा होता है।
- π = २२ ⁄ ७ अर्थात् ३·१४१६ की गणना।
- आर्यभट्ट ने दशमिक पद्धति ( decimal system ) का प्रयोग किया है। यह प्रथम नौ संख्याओं के स्थानीय मान और शून्य पर आधृत था।
वराहमिहिर
इनके पिता का नाम आदित्यदास और माता का नाम सत्यवती था। इनका जन्म कापित्यथका ( कायथा ) ग्राम, उज्जैन; म॰प्र० में हुआ था। ये ज्योतिष और गणित के विद्वान थे।
वराहमिहिर ने अपने पिता की स्मृति में ‘कापित्यका गुरुकुल’ की स्थापना की। यह गणित के इतिहास में ‘उज्जैन विद्यालय’ के नाम से प्रसिद्ध है। ब्रह्मगुप्त, महावीराचार्य, भास्कराचार्य आदि गणितज्ञ इसी गुरुकुल की देन हैं।
कंक- ७७० ई॰ के आसपास कंक नामक गणितज्ञ उज्जैन से बगदाद तत्कालीन ख़लीफ़ा अलमंसूर के निमंत्रण पर गये थे। कंक के माध्यम से में भारतीय गणित और ज्योतिष अरब जगत में पहुँची। कंक की सहायता से ब्रह्मगुप्त के ‘ ब्रह्मस्फुट सिद्धान्त’ का अरबी में अनुवाद किया गया।
ब्रह्मगुप्त
इनका जन्म राजस्थान के भीनमाल में ५९८ ई॰ में हुआ था।
ब्रह्मगुप्त ( लगभग ७वीं शताब्दी ) की प्रसिद्ध कृति ‘ब्रह्मस्फुट सिद्धान्त’ और ‘खण्डखाद्य’ है। ब्रह्मस्फुट सिद्धान्त में वृत्तीय चतुर्भुजों, वर्गों, आयतों आदि की परिभाषा एवं व्याख्या के अनेक सूत्र दिये गये हैं। उन्होंने वृत्तीय चतुर्भुजों के क्षेत्रफल, टॉलेमी प्रमेय, सूची स्तम्भ ( Pyramid ) और छिन्नक ( Frustum ) के आयतन का वर्णन किया गया है।
महावीर
महावीर ( ९वीं शताब्दी ) एक जैनधर्मावलम्बी गणितज्ञ थे। इनकी कृति ‘गणितसार संग्रह’ है। इन्होंने वृत्तों का क्षेत्रफल निकालने की विधि प्रस्तुत किया। धनात्मक और ऋणात्मक परिणामों से वे परिचित थे, वर्गमूल और घनमूल निकालने की ठोस प्रणाली का प्रवर्त्तन किया तथा वर्ग समीकरण एवं अन्य प्रकार के अनिश्चित समीकरणों का हल निकालने में निपुण थे।
गणित के महत्त्व के विषय में वे लिखते हैं — ‘गणित सांख्यिकी के रूप में अर्थशास्त्र की आँख है, भौतिकी की आत्मा है, प्रक्षेपण अस्त्र के रूप में सुरक्षा साधन है, ज्योतिष के रूप में लौकिक और पारलौकिक ज्ञाता साधन है, त्रिकोणमिति के रूप में आकाशीय गति का माध्यम है, अंकगणित के रूप में लोक व्यवहार का साधन है, वास्तुशास्त्र के रूप में नाप-जोख का साधना है, वाणिज्य में व्यापार का माध्यम है।’
भास्कर
इनका जन्म महाराष्ट्र में १११४ ई॰ में हुआ था।
गणितज्ञ भास्कर ( १२वीं शताब्दी ) की सुप्रसिद्ध कृति ‘सिद्धान्त सिरोमणि’ है। इस कृति के चार भाग हैं :— लीलावती, बीजगणित, ग्रहगणित और गोला। लीलावती के ‘क्षेत्र व्यवहार’ अध्याय में भास्कर ने निम्न प्रकरणों पर लिखा है —
- समकोण त्रिभुजों पर प्रश्न,
- त्रिभुजों एवं चतुर्भुजों के क्षेत्रफल,
- वृत्तों के क्षेत्रफल,
- π का मान,
- गोलों के तल और आयतन।
भास्कर ने ‘शुल्व प्रमेय’ ( बौधायन-पाइथागोरस प्रमेय ) की उपपत्ति दी है।
लीलावती अंकगणित और महत्त्वमानव ( क्षेत्रफल, घनफल ) का स्वतंत्र ग्रंथ है। इसमें पूर्णांक और भिन्न, त्रैराशिक ( Rule of three ) , व्यापार गणित, मिश्रण, श्रेणियाँ ( Series ), क्रमचय ( Permutation ), मापिकी ( Mensuration ) और कुछ बीजगणित भी है।
लीलावती को ‘पाटी गणित’ भी कहते हैं।
जिस अनिर्णीत समीकरणों ( Indeterminate equations ) की शुरुआत आर्यभट्ट ने की थी उसे भास्कर ने चरम पर पहुँचा दिया। भास्कर ने अनिर्णीत समीकरणों के हल की जो विधि दी है, उसको चक्रवाल विधि ( Cyclic method ) कहते हैं। इस विधि को पश्चिमी विद्वान ने १६वीं शती में जाना।
बीजगणित ग्रंथ में धनर्ण ( धनात्मक ) संख्याओं का योग, करणी ( Surds ) संख्याओं का योग, कुट्टक ( भाजक और भाज्य ) की प्रक्रिया, वर्ग प्रकृति, एक-वर्ग समीकरण, अनेक-वर्ग समीकरण आदि विषय वर्णित हैं।
सिद्धान्त शिरोमणि में ‘निरन्तर गति का विचार’ ( Idea of perpetual motion ) दिया गया है। कालान्तर में इसी से ‘शक्ति तकनीकी’ ( Power technology ) का विकास हुआ।
न्यूटन से शताब्दियों पूर्व ‘गुरुत्वाकर्षण सिद्धान्त’ का पता भास्कर ने लगा लिया था :—
“आकृष्ट शक्तिश्च मही तथा यत् स्वस्थं गुरु स्ंबाभिमुखं स्वशक्तया।
आकृष्टयते तत् पततीव भाति समे समन्तात् क्वं पतत्वियं खे॥”
( अर्थात् पृथ्वी में आकर्षण शक्ति है जिसके द्वारा वह सभी वस्तुओं को अपनी ओर खींचती है। वह जिसे खींचती है वह वस्तु भूमि पर गिरती हुई प्रतीत होती है। )
भास्कर शून्य और अनन्त का निहितार्थ समझते थे। गणित द्वारा उन्होंने सिद्ध किया कि शून्य वस्तुतः अनन्त है जो कभी विभाजित नहीं होता है। शून्य को किसी राशि में जोड़नेवाली इसमें कोई राशि जोड़ने या घटाने से राशि चिह्न में कोई परिवर्तन नहीं होता है। वे लिखते हैं :—
खयोगे वियोगे धनर्ण तथैव च्युत शून्यतस्तद्विपर्यासमेति॥
शून्य को किसी राशि में गुणा करने पर गुणनफल शून्य रहेगा परन्तु, शून्य से भाग देने पर ‘खहर’ या ‘खछेद’ होता है। यही खहर वर्तमान का ‘अनन्त’ ( ∞ ) है। इस तरह शून्य का कितना ही विभाजन किया जाय वह अनन्त ही रहेगा। भास्कर इसे इस तरह लिखते हैं :—
( ∞ ⁄ Χ = ∞ )
भारतीय गणितज्ञ
| क्रमांक | गणितज्ञ का नाम | समय | रचना |
| १. | बौधायन | ८०० ई॰पू॰ | शुल्व सूत्र |
| २. | आर्यभट्ट-प्रथम | ४७६ – ५५० ई॰ | आर्यभट्टीयम् |
| ३. | वराहमिहिर | ५५० – ५८७ ई॰ | पंचसिद्धान्तिका |
| ४. | जिनभद्र गणि | ५७५ ई॰ | विशेषवास्यक भाष्य |
| ५. | ब्रह्मगुप्त | ५९८ ई॰ | ब्रह्मस्फुट सिद्धान्त |
| ६. | भास्कर-प्रथम | ६२९ ई॰ | महाभास्करीय, लघुभास्करीय |
| ७ | श्रीधराचार्य | ७५० ई॰ | पाटी गणित, त्रिशतिका |
| ८. | वीरसेन | ७१० – ७९० ई॰ | धवलाटीका |
| ९. | महावीराचार्य | ८५० ई॰ | गणितसार संग्रह |
| १०. | गोविंद स्वामी | ८०० – ८५० ई॰ | महाभाष्करीय पर टीका |
| ११. | पृथुदक स्वामी | ८५० ई॰ | ब्रह्मसिद्धांतवासना भाष्य |
| १२. | वटेश्वराचार्य | ९०४ ई॰ | वटेश्वर सिद्धान्त |
| १३. | आर्यभट्ट-द्वितीय | ९५० ई॰ | महासिद्धान्त |
| १४. | श्रीपति | १०३९ – १०५६ ई॰ | गणित तिलक |
| १५. | भास्कराचार्य-द्वितीय | १११४ – ११९३ ई॰ | सिद्धान्त शिरोमणि, लीलावती |
| १६. | माधावाचार्य | १३४० – १४२५ ई॰ | चन्द्रवाक्यानि |
| १७. | नारायण पंडित | १३५६ ई॰ | गणित कौमुदी |
| १८. | परमेश्वराचार्य | १३६० – १४५५ ई॰ | लीलावती सूत्र |
| १९. | नीलकंठ सोमसुतवन | १४४४ – १५४५ ई॰ | तंत्र संग्रह |
| २०. | ज्येष्ठदेव | १५०० – १६१० ई॰ | युक्तिभाषा |
| २१. | शंकर वरियावर | १५०० – १५६० ई॰ | क्रियाक्रमकरी |
| २२. | पुतुमन सोमयाजी | १६६० – १७४० ई॰ | करण पद्धति |
| २३. | शंकरवर्मन् | १८०० – १८३८ ई॰ | सद्-रत्नमाला |
| २४. | स्वामी भारतीकृष्ण तीर्थ | १८८४ – १९६० ई॰ | वैदिक गणित |
| २५ | श्रीनिवास रामानुजन | १८८७ – १९२० ई॰ | संख्या सिद्धान्त |
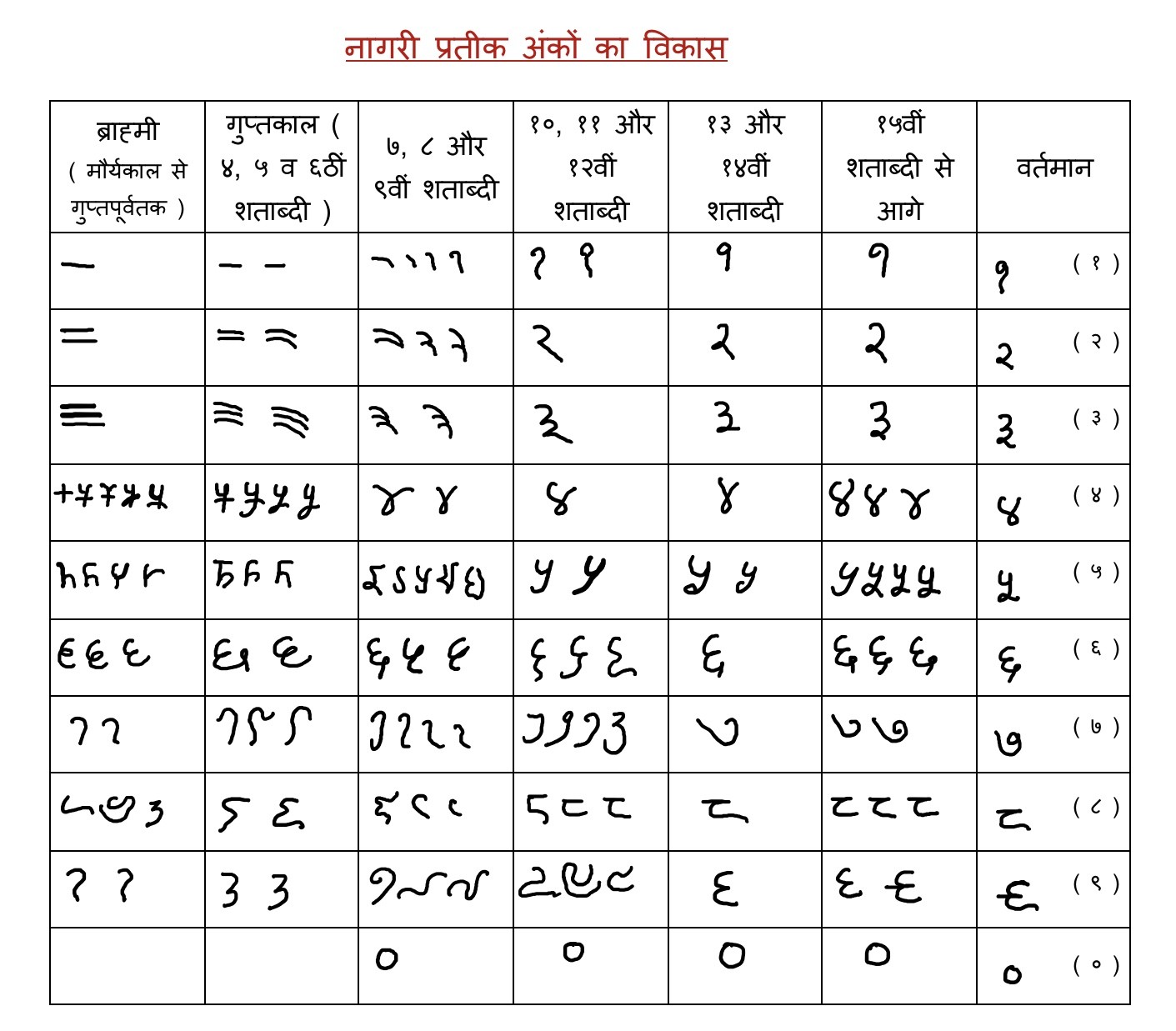
नागरी प्रतीक अंकों का विकास
नागरी प्रतीक अंकों का विकास ब्राह्मी अंकों से हुआ है।
नागरी लिपि के साक्ष्य हमें अशोक के अभिलेखों से मिलने लगते हैं।
प्राचीन शैली का समय मौर्यकाल से लेकर गुप्तपूर्व तक के समय तक के शामिल किया गया है। इस समय शून्य का पता न होने से उसका व्यवहार भी नहीं होता था। परिणामतः लोग १ से लेकर ९ तक के संकेतों का प्रयोग तो करते थे परन्तु १०, २०, ३० … आदि संकेतों का प्रयोग नहीं करते थे। दूसरे शब्दों में १, २, ३ आदि अंक संकेतों के साथ शून्य का प्रयोग नहीं करते थे।
शून्य की खोज कब और कैसे हुई अज्ञात है। परन्तु सम्भवतः चौथी-पाँचवीं शताब्दी में ( गुप्तकाल ) में इसके खोज होने पर विद्वानों में सहमति है। पूर्व में १०, २०, ३० … आदि के लिए जिन प्रतीकों का प्रयोग होता था उसे छोड़कर भारतीयों ने शून्य और अन्य नौ अंक प्रतीकों की सहायता से इन संख्याओं ( १०, २०, ३० … आदि ) को लिखने की सरल व वैज्ञानिक विधि का प्रयोग शुरु कर दिया।
अंक संकेतों की उत्पत्ति के संदर्भ में विभिन्न मत हैं :—
( १ ) अशोक के अभिलेखों को सबसे पहले पढ़ने वाले विद्वान ‘जेम्स प्रिंसेप’ का मत है कि ये अंक संकेत उन शब्दों से विकसित हुए जिन शब्दों से इन्हें व्यक्त किया जाता था; जैसे – एक के ‘ए’ से १ का विकास हुआ। परन्तु बूलर नामक विद्वान इसका विरोध करते हैं।
( २ ) दूसरा मत भाषाविद् ‘डॉक्टर भोलानाथ तिवारी’ का है। उनके अनुसार एक, दो और तीन का विकास तो एक अँगुली, दो अँगुली और तीन अँगुली के प्रतीक से क्रमशः हुआ। शेष प्रतीक चिह्नों का विकास यादृच्छिक तरीके से हुआ।
निष्कर्ष
भारत में इस अनन्तता की अनुभूति ब्रह्म अथवा आत्मा के सम्बन्ध में वेदान्तियों ने पहले ही कर ली थी :—
ॐ पूर्णमदः पूर्णमिदं पूर्णात् पूर्णमुदच्यते ।
पूर्णास्य पूर्णमादाय पूर्णमेवावशिष्यते ॥
( वृहदारण्यक उपनिषद् )
वस्तुतः शून्य और अनन्त ही आधुनिक गणित के आधार हैं।
भास्कर के बाद भारत में कोई मौलिक गणित लेखक नहीं हुआ। मुगलकाल में शेख फैजी ने लीलावती का फारसी में अनुवाद किया। तत्पश्चात् यह कृति अंग्रेजी में भी अनूदित हुई।
विद्वान ए॰ एल॰ बाशम गणित के क्षेत्र में भारतीयों की कृतज्ञता इस तरह व्यक्त करते हैं :—
“The debt of the Western world to India in this respect cannot be over-estimated. Most of the great discoveries and inventions of which Europe is so proud would have been impossible without a developed system of mathematics, and this in turn would have been impossible if Europe had been shackled by the unwieldy system of Roman numerals. The unknown man who devised the new system was from the world’s point of view, after the Buddha, the most important son of India. His achievement, though easily taken for granted, was the work of an analytical mind of the first order, and he deserves much more honour than he has so far received.”
( The Wonder That Was India, A. L. Basham )
“अंकन पद्धति, दाशमिक पद्धति और शून्य भारतीयों की विश्व को महानतम् देन है।”
प्राचीन भारत में विज्ञान का विकास